●目 的
放射性核種の半減期について理解を深め,放射性崩壊の特性を理解する。
●準 備
1円玉(1000枚=100枚×10班),箱または紙コップ,方眼紙,片対数方眼紙,電卓
(1円玉は,銀行に行って千円札を両替してもらえます。)
●実習1 放射性崩壊の模擬実験
(1)各班1円玉が100枚あることを確認。箱に100枚全部を表向き(向きがそろっていればOK)に入れる。
(2)箱のふたをしてよく振る。
(3)ふたを開けて,裏向きのものだけ取り出し,箱に残った枚数を数えて記録する。
裏向きのコインは,崩壊して別の原子核になったということ。
現在,造幣局では,作業上の必要性等から年号のある側を裏としています。
(4)もう一度ふたをしてよく振る。
(5)ふたを開けて,裏向きのものだけ取り出し,箱に残った枚数を数えて記録する。
この繰り返し
(6)最後に数枚になったら終了。黒板に記録を記入。
(7)グラフを作成する。縦軸は残った枚数,横軸は振った回数。
(8)教科書にある半減期のグラフと照らし合わせて,検討する。
(9)片対数グラフも作成する。
(10)10班分の合計も行う。
(11)100枚のときと1000枚のときで2種類のグラフはどのように違うか考える。
参考:改訂版新編物理ⅠB(平成14年数研出版)
●実習2 サイコロをモデルにした半減期予想と計算機実験
次のようなモデルを考える。
サイコロ(放射性核種)が多数あるとする。
同時にすべてのサイコロを振り,「1」が出たら崩壊し,別の原子核に変わったとする。つまり「1」が出たらサイコロを取り除く。
1分に1回サイコロを振るとする。
ただし ln2=0.693147 ,ln5=1.609437 ,ln6=1.791759
(12)このとき,サイコロの半減期は何分か。
(13)計算機を使って調べてみよう。
●発展問題
235U(半減期T=4.5×109年)が1モルある。この原子が最初に1個崩壊するのに要する時間は何秒か。また初めの1秒で崩壊する原子の数は何個か。
226Ra(半減期T=1.6×103年)ではどうか。
Windowsに着いている電卓は関数電卓にできる。
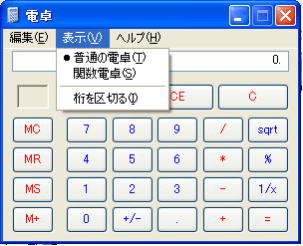
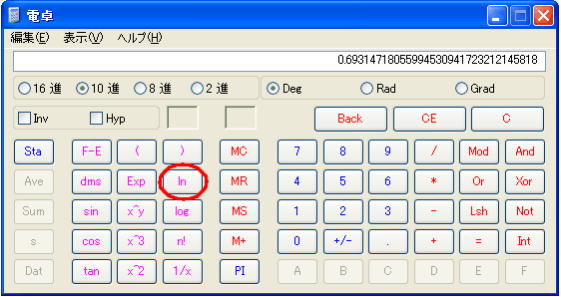
丸囲みのボタンは自然対数(底がeの対数 ln)である。
右図は ln2 の値。 2 の次に ln を押すと得られる。